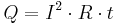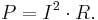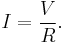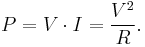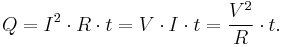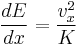Joule's laws
Joule's laws are a pair of laws concerning the heat produced by a current and the energy dependence of an ideal gas to that of pressure, volume, and temperature, respectively. They are named after James Prescott Joule.
Joule's first law, also known as the Joule effect, is a physical law expressing the relationship between the heat generated by the current flowing through a conductor. Joule studied this phenomenon in the 1840s. It is expressed as:
where  is the heat generated by a constant current
is the heat generated by a constant current  flowing through a conductor of electrical resistance
flowing through a conductor of electrical resistance  , for a time
, for a time  . When current, resistance and time are expressed in amperes, ohms, and seconds respectively, the unit of
. When current, resistance and time are expressed in amperes, ohms, and seconds respectively, the unit of  is the joule. Joule's first law is sometimes called the Joule–Lenz law since it was later independently discovered by Heinrich Lenz. The heating effect of conductors carrying currents is known as Joule heating.
is the joule. Joule's first law is sometimes called the Joule–Lenz law since it was later independently discovered by Heinrich Lenz. The heating effect of conductors carrying currents is known as Joule heating.
Joule's second law states that the internal energy of an ideal gas is independent of its volume and pressure, depending only on its temperature.
Contents |
Relation to Ohm's law
In the context of resistive circuits and in light of conservation of energy and electrical potential, Joule's first law and Ohm's law are equivalent and derivable from each other (as explained by James Clerk Maxwell in 1881,[1] by Mascart in 1883,[2] and by Oliver Heaviside in 1894[3]), though they were discovered independently and experimentally, before the notions of conservation of energy and electrical potential were well developed.
Joule's first law states that the rate of heat dissipation in a resistive conductor is proportional to the square of the current through it and to its resistance. That is, the power dissipated in a resistor, in terms of the current through it and its resistance, is:[4]
Joule arrived at this result experimentally in 1841, using a calorimeter to measure heat, and a galvanometer to measure current, with a variety of resistive circuits.[5][6]
The law applies to any circuit that obeys Ohm's law, that is, that conducts a current proportional to the voltage across it, or equivalently, that can be characterized by a resistance. Ohm's law states that for a voltage V across a circuit of resistance R the current will be:[7][8]
By substituting this formula for current into one or both factors of current in Joule's law, the power dissipated can be written in the equivalent forms:
The relation 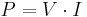 is actually more generally applicable than either Joule's law or Ohm's law, as it represents the instantaneous power being applied to a circuit with voltage V across it and current I into it, whether the circuit is resistive or not.[1][9] In combination with either Ohm's law or Joule's law, it may be used to derive the other.[10]
is actually more generally applicable than either Joule's law or Ohm's law, as it represents the instantaneous power being applied to a circuit with voltage V across it and current I into it, whether the circuit is resistive or not.[1][9] In combination with either Ohm's law or Joule's law, it may be used to derive the other.[10]
Since the power dissipated by a resistor is the amount of energy used (electrical work applied) per unit time, the total energy consumed and dissipated in time t is:[11]
Hydraulic equivalent
In the energy balance of groundwater flow (see also Darcy's law) an hydraulic equivalent of Joule's law is used [12] :
where:
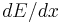 = loss of hydraulic energy (
= loss of hydraulic energy ( ) due to friction of flow in
) due to friction of flow in  -direction per unit of time (m/day) – comparable to
-direction per unit of time (m/day) – comparable to 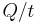
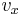 = flow velocity in
= flow velocity in  -direction (m/day) – comparable to
-direction (m/day) – comparable to 
 = hydraulic conductivity of the soil (m/day) – the hydraulic conductivity is inversely proportional to the hydraulic resistance which compares to
= hydraulic conductivity of the soil (m/day) – the hydraulic conductivity is inversely proportional to the hydraulic resistance which compares to 
See also
Notes
- ^ a b James Clerk Maxwell with William Garnett (ed.) (1881). An elementary treatise on electricity. Clarendon press. p. 100.
- ^ Éleuthère Élie N. Mascart, Jules F. Joubert (1883). A Treatise on Electricity and Magnetism. p. 238. http://books.google.com/books?id=iJQAAAAAMAAJ&pg=PA238&dq=%22ohm%27s+law%22+%22conservation+of+energy%22+potential+%22joule%27s+law%22+date:0-1884#PPA238,M1.
- ^ Ido Yavetz (1995). From Obscurity to Enigma. Birkhäuser. pp. 127–128. ISBN 9783764351809. http://books.google.com/books?id=SQszfj7biVMC&pg=PA128&dq=%22joule%27s+law%22+%22ohm%27s+law%22+%22conservation+of+energy%22+%22potential+difference%22+energy#PPA127,M1.
- ^ William Francis Magie (1911). Principles of Physics: Designed for Use as a Textbook of General Physics. New York: The Century Co. p. 508. http://books.google.com/books?id=UVZDAAAAIAAJ&pg=PA508&dq=%22joule%27s+law%22+I2R.
- ^ James Clerk Maxwell (1881). A Treatise on Electricity and Magnetism. II (2nd ed.). Oxford: Clarendon. p. 377. http://books.google.com/books?id=jAgXAAAAYAAJ&pg=PA377&dq=current+square+%22joule%27s+law%22+date:0-1900.
- ^ William Watson and Herbert Moss (1920). A Text-book of Physics. Longmans, Green, and Co. p. 708. http://books.google.com/books?id=EzVJAAAAIAAJ&pg=PA708&dq=%22joule%27s+law%22+%22proportional+to+the+square+of+the+current%22.
- ^ Clarence V. Christie (1917). Electrical Engineering: The Theory and Characteristics of Electrical Circuits and Machinery (2nd ed.). McGraw-Hill. p. 79. http://books.google.com/books?id=XMxIAAAAMAAJ&pg=PA79&dq=current+square+%22joule%27s+law%22+%22ohm%27s+law%22+resistance.
- ^ Ejup N. Ganic and Tyler G. Hicks (2002). McGraw-Hill's Engineering Companion. McGraw-Hill Professional. p. 16.3–16.5. ISBN 9780071378369. http://books.google.com/books?id=hld7ft72bzEC&pg=PT642&dq=applicable+%22joule%27s+law%22+%22ohm%27s+law%22#PPT644,M1.
- ^ Oliver Heaviside (1894). Electrical Papers. 1. Macmillan and Co. p. 305. http://books.google.com/books?id=lKV-AAAAMAAJ&pg=PA305&dq=%22joule%27s+law%22+%22ohm%27s+law%22+%22conservation+of+energy%22+potential.
- ^ Joseph Slabey Rouček (1971). The Challenge of Science Education. Ayer Publishing. p. 166. http://books.google.com/books?id=XNryx4KyPjEC&pg=PA166&dq=%22ohm%27s+law%22+%22joule%27s+law%22+derive.
- ^ Charles MacCaughey Sames (1906). A Pocket-book of Mechanical Engineering. C. M. Sames. p. 131. http://books.google.com/books?id=tZ4NAAAAYAAJ&pg=PA131&dq=%22joule%27s+law%22+I2R.
- ^ R.J.Oosterbaan, J.Boonstra and K.V.G.K.Rao (1996). The energy balance of groundwater flow. In: V.P.Singh and B.Kumar (eds.), Subsurface-Water Hydrology, Vol.2 of the Proceedings of the International Conference on Hydrology and Water Resources, New Delhi, India. Kluwer Academic Publishers, Dordrecht, The Netherlands. pp. 153–160. ISBN 978-0-7923-3651-8. http://www.waterlog.info/pdf/enerbal.pdf.